Una parábola en matemáticas es una curva fascinante que se encuentra en diversas aplicaciones, desde la geometría hasta la física. Esta curva abierta y continua se define como el conjunto de todos los puntos que están a la misma distancia de un punto fijo, conocido como foco, y de una línea recta fija, llamada directriz. Además, la parábola es una sección cónica que resulta de la intersección de un cono circular recto con un plano que es paralelo a una de sus generatrices.
Entender la parábola es esencial para profundizar en temas más complejos de las matemáticas y sus aplicaciones en el mundo real. A lo largo de este artículo, exploraremos su definición, propiedades fundamentales, ecuaciones y ejemplos prácticos que ilustran cómo esta curva se manifiesta en la arquitectura y la ingeniería.
Puntos clave:- La parábola es una curva que se define por su relación con un foco y una directriz.
- Se puede representar gráficamente y tiene propiedades importantes como la simetría y el eje de la parábola.
- La ecuación estándar de la parábola permite describir su forma y características matemáticas.
- Las parabolas tienen aplicaciones prácticas en arquitectura, como en la construcción de arcos y estructuras.
- En física, las parabolas son fundamentales para entender el movimiento de proyectiles y otras dinámicas.
Definición clara de la parábola en matemáticas y sus características
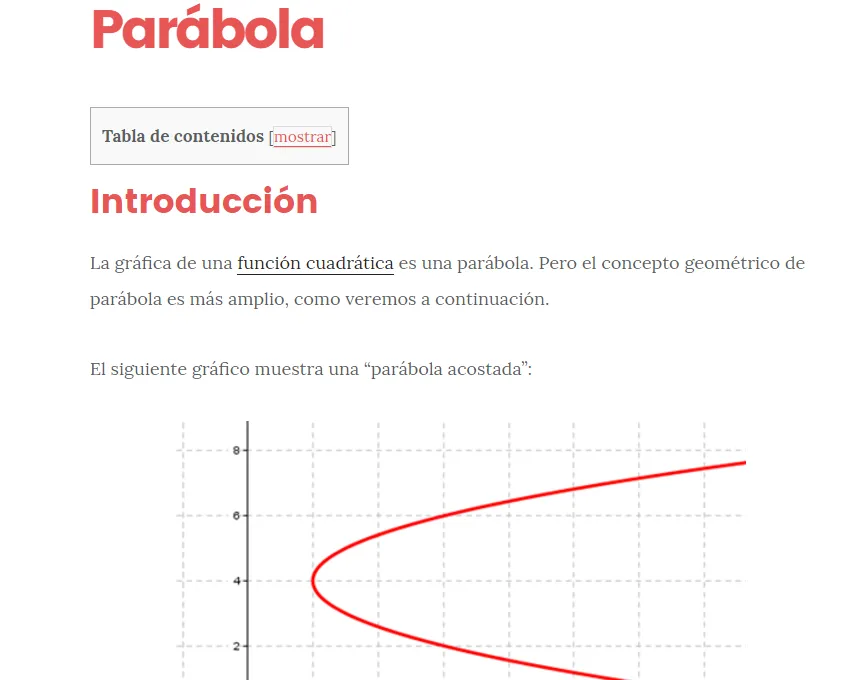
Una parábola en matemáticas es una curva abierta y continua. Esta curva se forma cuando todos los puntos de la misma están a la misma distancia de un punto fijo, conocido como foco, y de una línea recta fija, llamada directriz. La parábola se puede visualizar en un gráfico, donde su forma característica se asemeja a un "U" o a un "V". Esta representación gráfica es fundamental para comprender cómo se comporta la parábola en diferentes contextos matemáticos.
Además, la parábola puede ser considerada como una sección cónica que resulta de la intersección de un cono circular recto con un plano que es paralelo a una de sus generatrices. Esta definición geométrica proporciona una base sólida para explorar las propiedades y aplicaciones de la parábola en diversas áreas de las matemáticas y la ciencia.¿Qué es una parábola y cómo se representa gráficamente?
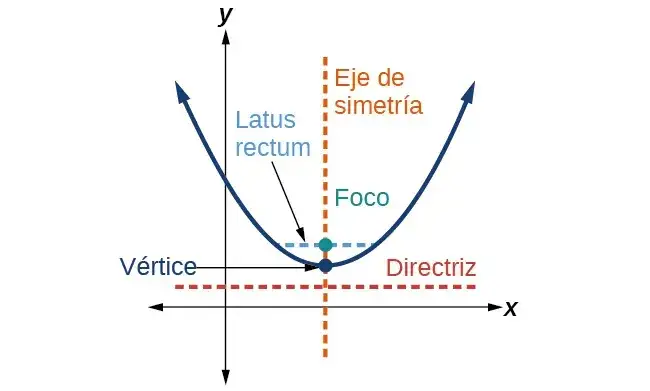
La parábola es un tipo de curva que se puede representar de manera gráfica utilizando un sistema de coordenadas. Para graficar una parábola, se necesita identificar su vértice, que es el punto más bajo o más alto de la curva, dependiendo de su orientación. También es importante localizar el foco y la directriz, ya que estos elementos son fundamentales para definir la forma de la parábola. La gráfica de una parábola puede abrirse hacia arriba, hacia abajo, a la derecha o a la izquierda, dependiendo de la ecuación que la describa.
- El vértice es el punto donde la parábola cambia de dirección.
- El foco es un punto dentro de la parábola que influye en su forma.
- La directriz es una línea recta que ayuda a definir la curva de la parábola.
Propiedades fundamentales de la parábola en matemáticas
Las propiedades de la parábola en matemáticas son esenciales para comprender su comportamiento y características. Una de las propiedades más importantes es el foco, que es el punto fijo dentro de la parábola desde el cual se mide la distancia a cualquier punto de la curva. Este foco determina la forma de la parábola y es crucial para su definición. Otra propiedad clave es la directriz, que es una línea recta que se encuentra fuera de la parábola y también se utiliza para definir la curva.
Además, la parábola tiene un eje de simetría, que es una línea imaginaria que divide a la parábola en dos mitades iguales. Esta simetría es fundamental para analizar la forma y la ubicación de la parábola en un sistema de coordenadas. Por último, la apertura de la parábola puede ser hacia arriba, hacia abajo, a la derecha o a la izquierda, dependiendo de la orientación de su ecuación. Estas propiedades son fundamentales para entender cómo se forma una parábola y su aplicación en diversas áreas de las matemáticas.
Ecuaciones de la parábola: Comprendiendo su forma y uso
Las ecuaciones de la parábola son fundamentales para describir su forma y comportamiento en un sistema de coordenadas. La ecuación más común es la ecuación estándar, que se presenta generalmente como \( y = ax^2 + bx + c \). En esta ecuación, el coeficiente \( a \) determina la apertura y la dirección de la parábola: si es positiva, la parábola se abre hacia arriba, y si es negativa, hacia abajo. Además, los valores de \( b \) y \( c \) afectan la posición de la parábola en el plano cartesiano, influyendo en su vértice y su intersección con el eje y.
Comprender la forma de esta ecuación es crucial para resolver problemas relacionados con las parabolas en matemáticas. Por ejemplo, al graficar la ecuación, se pueden identificar fácilmente sus características clave, como el vértice y el eje de simetría. Esto no solo ayuda en el ámbito académico, sino que también es útil en aplicaciones prácticas en campos como la física y la ingeniería, donde las trayectorias de los proyectiles a menudo siguen una forma parabólica.
Ecuación estándar de la parábola y su significado
La ecuación estándar de la parábola es una representación matemática que permite describir su forma y ubicación en el plano. Generalmente, se presenta en la forma \( (y - k) = a(x - h)^2 \), donde \( (h, k) \) es el vértice de la parábola. Esta forma es especialmente útil porque facilita la identificación de las características de la parábola, como su dirección de apertura y su vértice. Además, el valor de \( a \) en esta ecuación no solo determina la dirección de apertura, sino también la "anchura" de la parábola: un valor absoluto mayor de \( a \) resulta en una parábola más estrecha, mientras que un valor menor produce una más ancha.
Cómo se deriva la ecuación de la parábola
Derivar la ecuación de la parábola implica comprender su definición geométrica. Para ello, se considera la distancia entre un punto en la parábola y el foco, así como la distancia a la directriz. Usando la definición de la parábola como el conjunto de puntos equidistantes de estos dos elementos, se puede establecer una relación algebraica. Al aplicar la fórmula de la distancia y simplificar, se obtiene la ecuación estándar. Este proceso no solo ayuda a entender la forma de la parábola, sino que también proporciona una base para resolver problemas más complejos en matemáticas y física.| Forma de la Ecuación | Descripción |
|---|---|
| Ecuación estándar | (y - k) = a(x - h)^2 |
| Ecuación general | y = ax^2 + bx + c |
Read More: Cómo es el signo de mayor en matemáticas y su uso en desigualdades
Aplicaciones prácticas de la parábola en la vida real
Las parabolas en matemáticas tienen múltiples aplicaciones prácticas en diversas disciplinas, incluyendo la arquitectura, el diseño, la física y la ingeniería. Un ejemplo icónico es el Gateway Arch en St. Louis, que es una estructura monumental en forma de parábola. Este diseño no solo es estéticamente atractivo, sino que también proporciona estabilidad y resistencia, aprovechando las propiedades de la curva para distribuir el peso de manera eficiente. Además, las parabolas se utilizan en la construcción de puentes y arcos, donde su forma ayuda a soportar cargas pesadas.
En el ámbito de la ingeniería, las parabolas son esenciales en la construcción de satélites y antenas parabólicas. Estas estructuras utilizan la forma parabólica para concentrar señales de radio y mejorar la recepción de datos. La forma de la parábola permite que las ondas se reflejen hacia un punto focal, donde se encuentra el receptor. Esto maximiza la eficiencia de la transmisión y recepción de señales, lo que es crucial en la comunicación moderna y la transmisión de información.
| Aplicación | Descripción |
|---|---|
| Gateway Arch | Estructura en forma de parábola que simboliza la ciudad de St. Louis. |
| Antenas parabólicas | Diseñadas para concentrar señales de radio y mejorar la recepción. |
Ejemplos de parabolas en arquitectura y diseño
Las parabolas en arquitectura son utilizadas para crear estructuras tanto funcionales como estéticamente agradables. Un ejemplo notable es el Estadio Olímpico de Beijing, cuyo diseño incorpora elementos parabólicos que no solo aportan belleza, sino que también optimizan la acústica y la visibilidad. Otro ejemplo es el Pabellón de la Música en Valencia, donde las formas parabólicas permiten una mejor distribución del sonido, creando un ambiente acústico ideal para conciertos. Estas estructuras muestran cómo la geometría de la parábola puede ser aprovechada para mejorar el rendimiento arquitectónico y la experiencia del usuario.
Uso de la parábola en la física y la ingeniería
En el ámbito de la física y la ingeniería, las parabolas juegan un papel crucial en el análisis de trayectorias. Por ejemplo, el movimiento de un proyectil sigue una trayectoria parabólica, lo que permite a los ingenieros calcular la distancia y el ángulo óptimos para el lanzamiento. Además, las antenas parabólicas son otro ejemplo de aplicación práctica, ya que utilizan la forma de la parábola para concentrar señales de radio en un punto focal, mejorando la recepción. Estos usos demuestran la importancia de las parabolas en la resolución de problemas prácticos y en el diseño de tecnologías modernas.
Innovaciones futuras en el uso de parabolas en tecnología
A medida que la tecnología avanza, el uso de parabolas en diversas aplicaciones está evolucionando, especialmente en el ámbito de las comunicaciones y la energía. Un área emergente es la utilización de antenas parabólicas en sistemas de comunicación satelital, donde se están desarrollando modelos más eficientes que no solo mejoran la recepción de señales, sino que también optimizan el uso de energía. Estas antenas están siendo diseñadas para ser más ligeras y compactas, lo que facilita su instalación en entornos urbanos y remotos.
Además, en el campo de la energía solar, se están implementando colectores solares parabólicos que concentran la luz solar hacia un punto focal, generando calor que puede ser utilizado para producir electricidad. Esta tecnología no solo aprovecha la forma parabólica para mejorar la eficiencia energética, sino que también representa un paso hacia fuentes de energía más sostenibles. Con el aumento de la demanda de soluciones energéticas limpias, el futuro de las parabolas en la tecnología parece prometedor, ofreciendo nuevas oportunidades para innovaciones que impacten positivamente en el medio ambiente.