En matemáticas, una función es una relación que conecta dos conjuntos: el dominio y el codominio. Cada elemento del dominio se relaciona con un único elemento del codominio, lo que significa que para cada entrada hay una salida específica. Comprender las funciones es fundamental no solo para resolver problemas matemáticos, sino también para aplicar estos conceptos en diversas disciplinas como la economía, la física y la ingeniería.
A lo largo de este artículo, exploraremos los diferentes tipos de funciones, sus características y sus aplicaciones en el mundo real. Desde funciones lineales hasta cuadráticas y polinómicas, cada una tiene un papel crucial en el desarrollo del pensamiento matemático y en la resolución de problemas prácticos. Además, aprenderemos sobre la importancia de la visualización de funciones a través de gráficos, lo que facilitará su comprensión y aplicación en situaciones cotidianas.
Puntos clave:- Las funciones son relaciones entre dos conjuntos donde cada elemento del dominio se asocia a un único elemento del codominio.
- Existen varios tipos de funciones, incluyendo lineales, cuadráticas y polinómicas, cada una con sus propias propiedades y aplicaciones.
- Las funciones son esenciales en diversas disciplinas, como la economía, la física y la ingeniería, donde se utilizan para modelar y resolver problemas.
- La visualización de funciones a través de gráficos es crucial para entender su comportamiento y facilitar su interpretación.
- Realizar ejercicios prácticos ayuda a reforzar el aprendizaje y la identificación de funciones en diferentes contextos.
Definición de funciones matemáticas y su importancia educativa
En matemáticas, una función es una relación entre dos conjuntos donde cada elemento del primer conjunto, conocido como dominio, se asocia a un único elemento del segundo conjunto, llamado codominio. Esta relación se representa comúnmente como f(x), donde "f" es el nombre de la función y "x" es un elemento del dominio. Las funciones son fundamentales en el estudio de las matemáticas, ya que permiten modelar situaciones y resolver problemas de manera estructurada.
La importancia educativa de las funciones radica en su capacidad para desarrollar el pensamiento lógico y analítico en los estudiantes. Comprender cómo funcionan las funciones en matemáticas no solo ayuda a resolver ecuaciones, sino que también es esencial para aplicar conceptos matemáticos en diversas áreas, como la ciencia, la economía y la ingeniería. A medida que los estudiantes avanzan en su educación, el dominio de las funciones se convierte en una herramienta clave para abordar problemas complejos y realizar análisis más profundos.
Tipos de funciones matemáticas y sus características
En matemáticas, existen varios tipos de funciones que se clasifican según sus propiedades y comportamientos. Las funciones más comunes incluyen las funciones lineales, cuadráticas y polinómicas. Cada una de estas funciones tiene características distintivas que las hacen útiles en diferentes contextos. Comprender estas diferencias es crucial para aplicar las funciones de manera efectiva en problemas matemáticos y en la vida real.
Las funciones lineales son aquellas que pueden representarse en una gráfica como una línea recta. Estas funciones tienen la forma y = mx + b, donde "m" es la pendiente y "b" es el intercepto en el eje y. Las funciones lineales son simples y se utilizan frecuentemente para modelar situaciones donde hay una relación constante entre dos variables. Un ejemplo de función lineal es el cálculo del costo de producción en una empresa, donde el costo total (y) puede expresarse como una función del número de unidades producidas (x).
Funciones lineales: propiedades y ejemplos prácticos
Las funciones lineales tienen propiedades clave, como la constante tasa de cambio y la simplicidad en su representación gráfica. La pendiente "m" determina la inclinación de la línea, mientras que el intercepto "b" indica dónde la línea cruza el eje y. Estas funciones son útiles en diversas aplicaciones, desde la economía hasta la física, ya que permiten realizar predicciones y análisis de tendencias.
Por ejemplo, si una empresa produce camisetas y el costo de producción por camiseta es de 10 euros, la función lineal que representa el costo total (C) en función del número de camisetas producidas (x) sería C(x) = 10x. Esto significa que si la empresa produce 100 camisetas, el costo total sería C(100) = 10 * 100 = 1000 euros.
Funciones cuadráticas: características y aplicaciones en la vida real
Las funciones cuadráticas son aquellas que se representan gráficamente como una parábola. Tienen la forma y = ax² + bx + c, donde "a", "b" y "c" son constantes y "a" no puede ser cero. Estas funciones son importantes porque pueden modelar situaciones donde la tasa de cambio no es constante, como en el caso de los movimientos de proyectiles. La forma de la parábola depende del valor de "a": si es positivo, la parábola abre hacia arriba; si es negativo, hacia abajo.
Un ejemplo real de una función cuadrática es el lanzamiento de un objeto al aire. Si se lanza una pelota desde una altura inicial de 2 metros con una velocidad inicial de 10 metros por segundo, la altura de la pelota en función del tiempo puede describirse mediante una función cuadrática. Esto permite predecir la altura máxima que alcanzará la pelota y el tiempo que tardará en caer al suelo.
Funciones polinómicas: exploración de grados y comportamientos
Las funciones polinómicas son una extensión de las funciones lineales y cuadráticas, y pueden tener uno o más términos. Se expresan como P(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀, donde "n" es el grado del polinomio y los coeficientes a pueden ser cualquier número real. A medida que aumenta el grado, las funciones polinómicas pueden exhibir comportamientos más complejos, como múltiples máximos y mínimos.
Un ejemplo de función polinómica es la función que describe el crecimiento de una planta en función del tiempo. Si la altura de la planta puede modelarse con un polinomio de tercer grado, se pueden identificar los momentos en que la planta crece más rápidamente o se estanca. Esto es útil para los agricultores y científicos que estudian el crecimiento de las plantas y la optimización de condiciones de cultivo.
| Tipo de función | Forma general | Ejemplo |
| Lineal | y = mx + b | Costo de producción: C(x) = 10x |
| Cuadrática | y = ax² + bx + c | Lanzamiento de un objeto |
| Polinómica | P(x) = aₙxⁿ + ... + a₀ | Crecimiento de una planta |
Funciones cuadráticas: características y aplicaciones en la vida real
Las funciones cuadráticas son un tipo de función polinómica de segundo grado que se representan gráficamente como una parábola. Tienen la forma general y = ax² + bx + c, donde "a", "b" y "c" son constantes y "a" no puede ser cero. Una característica distintiva de estas funciones es que pueden tener un máximo o un mínimo, dependiendo del signo de "a". Si "a" es positivo, la parábola abre hacia arriba, y si es negativo, hacia abajo. Esta propiedad permite modelar fenómenos donde la relación entre las variables no es constante, como en el caso del lanzamiento de un objeto.
Un ejemplo real de una función cuadrática se puede observar en el lanzamiento de una pelota. Supongamos que una pelota se lanza al aire desde una altura inicial de 1 metro con una velocidad inicial de 15 metros por segundo. La altura de la pelota en función del tiempo puede describirse mediante una función cuadrática, que permite predecir no solo la altura máxima que alcanzará, sino también el tiempo que tardará en volver al suelo. Esto es esencial en deportes como el baloncesto o el fútbol, donde entender la trayectoria del balón puede influir en el desempeño de los jugadores.
Funciones polinómicas: exploración de grados y comportamientos
Las funciones polinómicas son expresiones matemáticas que pueden tener uno o más términos y se representan como P(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀, donde "n" es el grado del polinomio y los coeficientes a pueden ser números reales. A medida que aumenta el grado del polinomio, la función puede exhibir comportamientos más complejos, como múltiples máximos y mínimos. Esto las convierte en herramientas poderosas para modelar una variedad de fenómenos en diferentes campos, desde la física hasta la economía.
Un ejemplo de función polinómica es el uso de un polinomio de tercer grado para modelar el crecimiento de una población de peces en un lago. Si se sabe que la tasa de crecimiento de la población puede describirse con una función cúbica, se pueden identificar los momentos en que la población alcanza su máximo y cuándo comienza a decrecer. Este tipo de análisis es crucial para la gestión de recursos naturales y la conservación de especies.
Read More: Todo lo que necesitas saber sobre la base en matemáticas y su uso
Aplicaciones esenciales de las funciones en diversas disciplinas
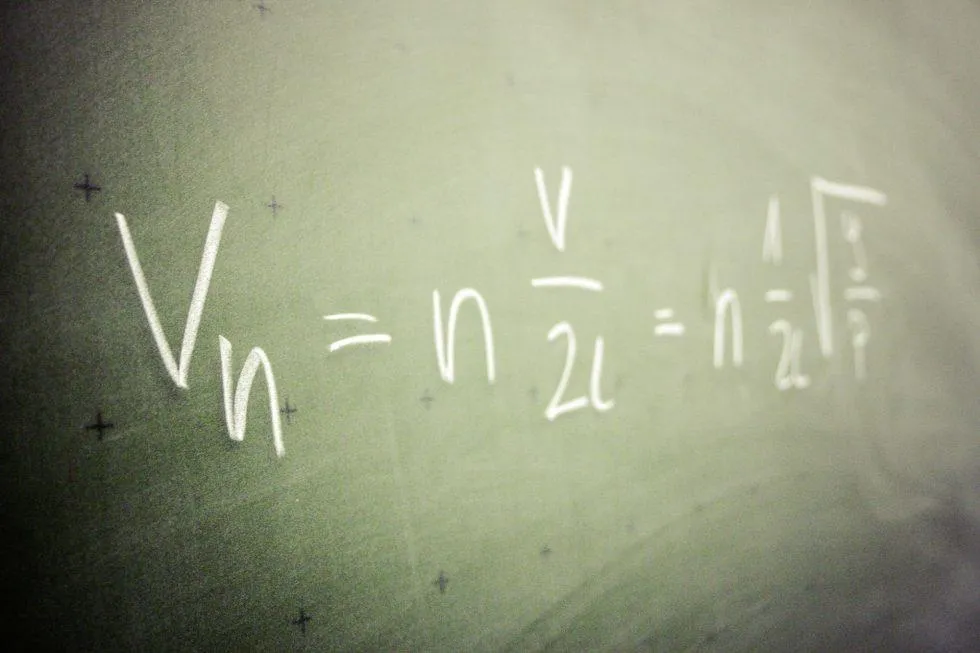Las funciones en matemática son herramientas fundamentales en diversas disciplinas, ya que permiten modelar situaciones y realizar análisis precisos. En campos como la economía, la física y la ingeniería, las funciones ayudan a describir relaciones entre variables y a predecir comportamientos. Comprender cómo aplicar estas funciones es crucial para la toma de decisiones informadas y la resolución de problemas complejos. A continuación, se explorarán ejemplos específicos de cómo se utilizan las funciones en estas áreas.
Uso de funciones en la economía y las ciencias sociales
En economía, las funciones son esenciales para analizar el comportamiento del mercado y la toma de decisiones. Las funciones de oferta y demanda, por ejemplo, permiten entender cómo se determinan los precios de los bienes y servicios. La función de demanda muestra la cantidad de un producto que los consumidores están dispuestos a comprar a diferentes precios, mientras que la función de oferta representa la cantidad que los productores están dispuestos a vender. Esta relación es crucial para los economistas al prever cambios en el mercado.
Un ejemplo real es el modelo de oferta y demanda en el mercado de automóviles. Si el precio de los automóviles baja, la función de demanda indica que más consumidores estarán dispuestos a comprar, lo que puede llevar a un aumento en las ventas. Por otro lado, si los costos de producción aumentan, la función de oferta puede mostrar que los productores reducirán la cantidad de automóviles disponibles, lo que afectará el precio en el mercado.
Funciones en la física: modelando fenómenos naturales
En física, las funciones son utilizadas para modelar fenómenos naturales y describir el comportamiento de sistemas físicos. Por ejemplo, la función que describe la trayectoria de un proyectil se puede expresar como una función cuadrática, que permite calcular la altura del proyectil en función del tiempo. Esta relación es fundamental para entender y predecir el movimiento de objetos en diferentes condiciones.
Un ejemplo de esto es el lanzamiento de un balón de fútbol. Al calcular su trayectoria, se pueden usar funciones para determinar la altura máxima que alcanzará y el tiempo que tardará en caer al suelo. Esto es especialmente útil en deportes, donde los jugadores deben anticipar la trayectoria del balón para realizar jugadas efectivas.
Aplicaciones de funciones en la ingeniería y tecnología
En ingeniería, las funciones son cruciales para el diseño y análisis de sistemas. Se utilizan para modelar estructuras, circuitos eléctricos y sistemas mecánicos, entre otros. Por ejemplo, las funciones pueden ayudar a calcular las fuerzas que actúan sobre una estructura, asegurando que sea segura y eficiente. Además, las funciones matemáticas permiten optimizar el rendimiento de sistemas tecnológicos, como en el caso de la programación de algoritmos en informática.
Un ejemplo real es el diseño de puentes. Los ingenieros utilizan funciones para calcular las cargas que el puente debe soportar y cómo distribuir esas cargas a lo largo de su estructura. Esto incluye el uso de funciones para modelar el comportamiento del material bajo diferentes condiciones, asegurando que el puente sea seguro y duradero.
- Las funciones de oferta y demanda son clave en la economía para prever cambios en el mercado.
- Las funciones cuadráticas modelan la trayectoria de proyectiles en física, ayudando a predecir su movimiento.
- En ingeniería, las funciones se utilizan para diseñar estructuras seguras y eficientes, como puentes.
Funciones en la física: modelando fenómenos naturales
En el ámbito de la física, las funciones son herramientas esenciales para modelar y comprender fenómenos naturales. Las funciones permiten describir cómo varían las magnitudes físicas en relación con otras, facilitando la predicción de comportamientos en sistemas físicos. Por ejemplo, la relación entre la distancia y el tiempo en un movimiento uniforme se puede expresar mediante una función lineal, mientras que el movimiento de un proyectil se describe a través de funciones cuadráticas. Estas representaciones matemáticas son fundamentales para el análisis y la resolución de problemas en la física.
Un ejemplo real es el estudio del movimiento de un proyectil lanzado al aire. Supongamos que se lanza una pelota desde una altura de 2 metros con una velocidad inicial de 10 metros por segundo. La altura de la pelota en función del tiempo puede describirse utilizando una función cuadrática, lo que permite calcular la altura máxima que alcanzará y el tiempo que tardará en volver al suelo. Este tipo de análisis es crucial en deportes y en aplicaciones de ingeniería donde se requiere entender la trayectoria de un objeto.
Aplicaciones de funciones en la ingeniería y tecnología
En el campo de la ingeniería y la tecnología, las funciones son fundamentales para el diseño y el análisis de sistemas complejos. Los ingenieros utilizan funciones matemáticas para modelar el comportamiento de estructuras, circuitos eléctricos y sistemas mecánicos, entre otros. Por ejemplo, las funciones permiten calcular las cargas que una estructura debe soportar, optimizando su diseño para garantizar la seguridad y la eficiencia. Esto es esencial en la creación de edificios, puentes y otras infraestructuras.
Un ejemplo específico es el diseño de un puente. Los ingenieros aplican funciones para calcular las fuerzas que actúan sobre la estructura, considerando factores como el peso del puente, la carga de vehículos y las condiciones climáticas. Mediante el uso de funciones, pueden prever cómo se comportará el puente bajo diferentes condiciones y asegurarse de que sea seguro y duradero. Este enfoque matemático es vital para la ingeniería moderna y la construcción de infraestructuras que soporten el paso del tiempo.
Innovaciones en modelado de funciones para la sostenibilidad
Las funciones matemáticas no solo son herramientas clave en la física y la ingeniería, sino que también están tomando un papel central en la búsqueda de soluciones sostenibles. Con el aumento de la conciencia sobre el cambio climático y la necesidad de prácticas más ecológicas, el modelado de funciones se está utilizando para optimizar recursos y minimizar el impacto ambiental. Por ejemplo, en el diseño de sistemas de energía renovable, las funciones pueden ayudar a predecir la producción de energía solar o eólica en función de variables como la ubicación, la hora del día y las condiciones climáticas.
Además, el uso de funciones polinómicas en el análisis de datos permite a los ingenieros y científicos ambientales simular escenarios futuros y evaluar el rendimiento de tecnologías sostenibles. Esto incluye la modelación de la absorción de CO2 en bosques o el análisis de la eficiencia de sistemas de reciclaje. Con el avance de la tecnología de big data y el aprendizaje automático, las funciones matemáticas se están integrando en algoritmos que pueden procesar grandes volúmenes de datos, ofreciendo así soluciones innovadoras y adaptativas para enfrentar los desafíos ambientales del futuro.
