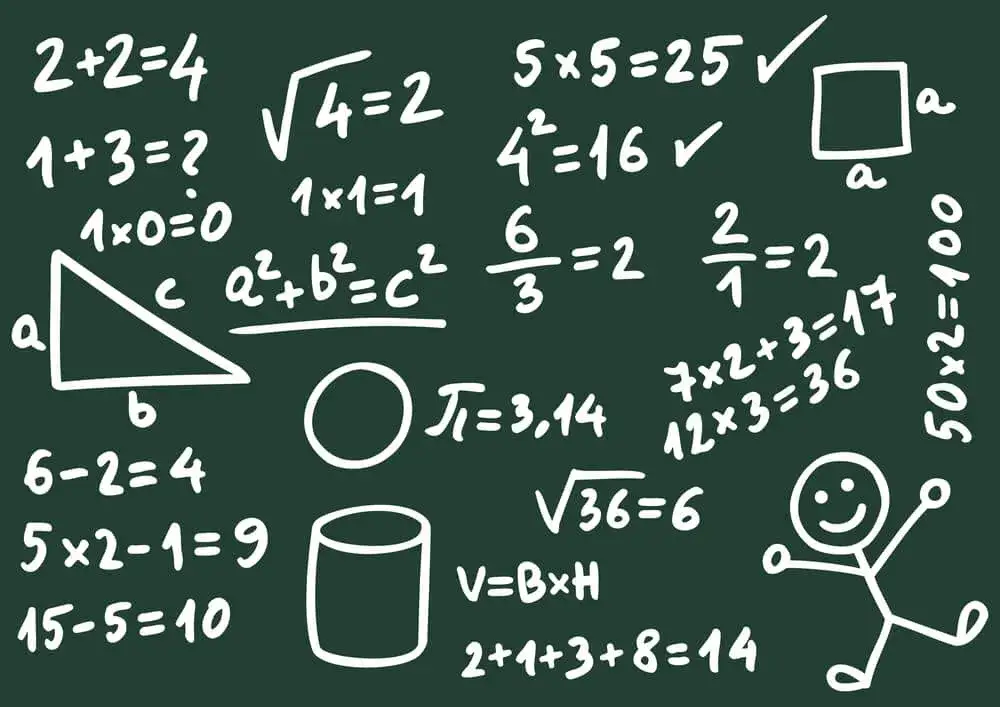Los símbolos matemáticos son herramientas esenciales en el mundo de las matemáticas, ya que nos permiten expresar operaciones, relaciones y conceptos de manera precisa y concisa. En este artículo, exploraremos 200 símbolos matemáticos en español que son fundamentales para entender mejor esta disciplina. Desde los símbolos más comunes, como la suma (+) y la resta (-), hasta aquellos menos conocidos, cada símbolo tiene su propio significado y aplicación.
Conocer estos símbolos no solo facilita la resolución de problemas matemáticos, sino que también mejora nuestra capacidad para comunicar ideas matemáticas de forma efectiva. A lo largo de este artículo, presentaremos un listado completo de símbolos, su clasificación y ejemplos visuales que ayudarán a los lectores a familiarizarse con ellos de manera más efectiva.
Conclusiones clave:- Los símbolos matemáticos son fundamentales para realizar operaciones y expresar relaciones en matemáticas.
- Existen símbolos básicos, como los de suma y resta, y otros más complejos utilizados en álgebra y cálculo.
- La representación gráfica de estos símbolos puede facilitar el aprendizaje y la comprensión de conceptos matemáticos.
- Recursos adicionales, como libros y plataformas en línea, son útiles para profundizar en el estudio de los símbolos matemáticos.
- Familiarizarse con los símbolos mejora la comunicación y la resolución de problemas en matemáticas.
Listado completo de símbolos matemáticos en español para aprender
Los símbolos matemáticos son herramientas fundamentales en el estudio de las matemáticas, ya que permiten representar operaciones, relaciones y conceptos de manera clara y concisa. Conocer estos símbolos es crucial para poder resolver problemas matemáticos y entender teorías complejas. En este artículo, se presenta una lista extensa de símbolos matemáticos en español, que incluye tanto los más comunes como aquellos menos conocidos, junto con su significado y uso en diferentes contextos.
La comprensión de los símbolos matemáticos no solo facilita la resolución de ecuaciones, sino que también mejora la comunicación de ideas matemáticas. A medida que avanzamos en el estudio de las matemáticas, es importante familiarizarnos con categorías de símbolos, que incluyen operaciones básicas, relaciones y funciones. A continuación, se ofrece una tabla con al menos 20 símbolos matemáticos, su representación y significado, para ayudar a los lectores a aprender de manera efectiva.
| Símbolo | Significado |
|---|---|
| + | Suma o adición. Indica la operación de sumar dos o más números. |
| - | Resta o sustracción. Representa la operación de restar un número de otro. |
| × | Multiplicación. Indica la operación de multiplicar dos o más números. |
| ÷ | División. Representa la operación de dividir un número entre otro. |
| = | Igualdad. Indica que dos expresiones son equivalentes. |
| ≠ | Diferente de. Indica que dos expresiones no son equivalentes. |
| > | Mayor que. Indica que una cantidad es mayor que otra. |
| < | Menor que. Indica que una cantidad es menor que otra. |
| ≥ | Mayor o igual que. Indica que una cantidad es mayor o igual a otra. |
| ≤ | Menor o igual que. Indica que una cantidad es menor o igual a otra. |
| √ | Raíz cuadrada. Indica la operación de encontrar la raíz cuadrada de un número. |
| ∑ | Sumatoria. Indica la suma de una serie de términos. |
| ∏ | Producto. Indica el producto de una serie de términos. |
| ∈ | Pertenece a. Indica que un elemento es parte de un conjunto. |
| ∉ | No pertenece a. Indica que un elemento no es parte de un conjunto. |
| ∅ | Conjunto vacío. Representa un conjunto que no contiene elementos. |
| ∞ | Infinito. Representa una cantidad sin límite. |
| ∫ | Integral. Indica la operación de integración en cálculo. |
| ∂ | Derivada parcial. Indica la derivada de una función respecto a una de sus variables. |
| ⊥ | Perpendicular. Indica que dos líneas son perpendiculares entre sí. |
| || | Paralelo. Indica que dos líneas son paralelas entre sí. |
| ∧ | Conjunción lógica. Representa la operación "y" en lógica. |
| ∨ | Disyunción lógica. Representa la operación "o" en lógica. |
Símbolos de relación y comparación en matemáticas
Los símbolos de relación y comparación son esenciales en matemáticas, ya que permiten establecer cómo se relacionan diferentes cantidades entre sí. Estos símbolos son fundamentales para entender conceptos como la igualdad, la desigualdad y las comparaciones numéricas. Sin ellos, sería difícil expresar y resolver problemas matemáticos de manera efectiva. Al conocer estos símbolos, los estudiantes pueden interpretar mejor las relaciones en ecuaciones y expresiones matemáticas.
Entre los símbolos más utilizados se encuentran: el signo de igual (=), que indica que dos expresiones son equivalentes; el signo mayor que (>) y menor que (<), que permiten comparar dos cantidades; y los símbolos de mayor o igual que (≥) y menor o igual que (≤), que son útiles en situaciones que involucran límites o rangos. Estos símbolos son clave en muchos contextos, desde la resolución de ecuaciones hasta la comparación de datos en gráficos.
- El símbolo "=" se usa para mostrar que dos cantidades son las mismas, por ejemplo, en la ecuación 2 + 2 = 4.
- El símbolo ">" se utiliza para indicar que una cantidad es mayor que otra, como en 5 > 3.
- El símbolo "<" muestra que una cantidad es menor que otra, como en 2 < 4.
- Los símbolos "≥" y "≤" se utilizan en contextos donde se requieren comparaciones que incluyen límites, como en las desigualdades.
Operadores aritméticos y su significado en español
Los operadores aritméticos son fundamentales en matemáticas, ya que nos permiten realizar las cuatro operaciones básicas: suma, resta, multiplicación y división. Cada uno de estos operadores tiene un símbolo específico que se utiliza para representar la operación correspondiente. Por ejemplo, el símbolo "+" se usa para la suma, mientras que el símbolo "-" se utiliza para la resta. La multiplicación se representa con "×" o "*", y la división se indica con "÷" o "/". Conocer estos operadores es esencial para resolver problemas matemáticos de manera efectiva.
Para ilustrar su uso, consideremos algunos ejemplos. En la suma, si tenemos 3 + 5, el resultado es 8. En la resta, 10 - 4 nos da 6. Para la multiplicación, 2 × 3 resulta en 6, y en la división, 12 ÷ 4 es igual a 3. Estos operadores son la base de muchas operaciones matemáticas más complejas y son vitales en el aprendizaje de las matemáticas.
Símbolos de álgebra y su aplicación en ecuaciones
Los símbolos de álgebra son esenciales para la representación de variables y constantes en ecuaciones matemáticas. Estos símbolos permiten expresar relaciones y operaciones de manera abstracta, lo que es fundamental para resolver problemas más complejos. Por ejemplo, "x" puede representar un número desconocido, mientras que "c" podría ser una constante. La correcta utilización de estos símbolos facilita la comprensión de conceptos algebraicos y la resolución de ecuaciones.
Un ejemplo de una ecuación que utiliza varios símbolos algebraicos es 2x + 3 = 11. En esta ecuación, "2x" representa el doble de la variable "x", y "3" es una constante. Para resolverla, restamos 3 de ambos lados, obteniendo 2x = 8, y luego dividimos entre 2, lo que nos da x = 4. Este tipo de ecuaciones es común en el álgebra y muestra cómo se utilizan los símbolos para encontrar soluciones.
Representación gráfica de símbolos matemáticos para facilitar el aprendizaje
La representación gráfica de símbolos matemáticos es una herramienta poderosa que puede mejorar significativamente la comprensión de conceptos matemáticos. Visualizar los símbolos ayuda a los estudiantes a asociar operaciones y relaciones con imágenes concretas, facilitando así el aprendizaje. Además, los gráficos y diagramas pueden simplificar la interpretación de datos y ecuaciones, haciendo que la información sea más accesible. Esta técnica es especialmente útil para aquellos que aprenden mejor de manera visual, ya que permite captar rápidamente las ideas fundamentales.
Utilizar gráficos para representar símbolos matemáticos también puede ayudar a identificar patrones y tendencias en los datos. Por ejemplo, al graficar funciones matemáticas, los estudiantes pueden observar cómo cambian los valores en función de las variables. Para crear gráficos efectivos, es importante elegir el tipo adecuado de representación visual, como gráficos de barras, líneas o dispersión, dependiendo de la información que se desea comunicar. A continuación, se presenta un consejo sobre cómo crear gráficos que representen símbolos matemáticos de manera efectiva.
Importancia de la visualización en el entendimiento matemático
Visualizar símbolos matemáticos es crucial para mejorar la comprensión y el aprendizaje de conceptos matemáticos. Cuando los estudiantes pueden ver cómo se relacionan los símbolos con representaciones gráficas, se facilita la asimilación de ideas complejas. La visualización ayuda a identificar patrones y conexiones que pueden no ser evidentes solo a través de la lectura de texto. Además, utilizar elementos visuales puede hacer que el aprendizaje sea más atractivo y menos intimidante.
La conexión entre visualización y comprensión se evidencia en diversas áreas de las matemáticas, desde la aritmética básica hasta el álgebra avanzada. Por ejemplo, al graficar una ecuación, los estudiantes pueden ver cómo cambian los valores a medida que se modifican las variables, lo que refuerza su entendimiento. Incorporar técnicas de visualización en el estudio diario puede ser una estrategia efectiva para mejorar la retención de información y la resolución de problemas. A continuación, se presenta un consejo sobre cómo implementar la visualización en el estudio de matemáticas.
Integrando tecnología en el aprendizaje de símbolos matemáticos
La incorporación de la tecnología educativa en el aprendizaje de símbolos matemáticos está revolucionando la forma en que los estudiantes comprenden y aplican estos conceptos. Herramientas como aplicaciones móviles, software de matemáticas y plataformas de aprendizaje en línea ofrecen entornos interactivos donde los estudiantes pueden practicar el uso de símbolos en contextos variados. Por ejemplo, programas que permiten la visualización dinámica de ecuaciones y gráficos ayudan a los estudiantes a experimentar con diferentes variables y observar resultados en tiempo real, facilitando un aprendizaje más profundo.
Además, el uso de realidad aumentada y realidad virtual en el aula puede llevar la visualización de símbolos matemáticos a un nuevo nivel. Estas tecnologías permiten a los estudiantes interactuar con representaciones tridimensionales de conceptos matemáticos, haciendo que el aprendizaje sea más inmersivo y atractivo. A medida que la educación se adapta a estas innovaciones, es probable que el dominio de los símbolos matemáticos se vuelva más accesible y efectivo, preparando mejor a los estudiantes para enfrentar desafíos matemáticos en el futuro.
