Un término en matemáticas es fundamental para entender cómo funcionan las expresiones matemáticas. Cada término puede ser un número, una variable, o una combinación de ambos, y se relaciona con operadores aritméticos como sumas, restas, multiplicaciones y divisiones. Conocer la definición y el papel de los términos es crucial para resolver problemas matemáticos y simplificar expresiones.
En este artículo, exploraremos en profundidad qué es un término en matemáticas y su importancia en las expresiones. Aprenderemos a identificar términos en diferentes contextos y cómo estos afectan los resultados de las operaciones matemáticas. También abordaremos los tipos de términos y sus características, lo que nos permitirá tener una comprensión más clara de su aplicación en álgebra y ecuaciones.
Información clave:- Un término es un elemento en una expresión matemática, que puede ser un número o una variable.
- Los términos se combinan con operadores aritméticos para formar expresiones más complejas.
- Identificar términos es esencial para resolver ecuaciones y simplificar expresiones.
- Los términos pueden ser homogéneos (con el mismo grado) o heterogéneos (con diferentes grados).
- Comprender la función de los términos ayuda a realizar operaciones matemáticas de manera más efectiva.
Definición clara de término en matemáticas y su función
En matemáticas, un término se refiere a cada uno de los elementos que componen una expresión matemática. Estos elementos pueden ser números, variables o una combinación de ambos. Además, los términos están relacionados con operadores aritméticos como sumas, restas, multiplicaciones y divisiones, que son esenciales para realizar cálculos y resolver ecuaciones.
La función de un término es actuar como una unidad básica dentro de una expresión más compleja. Cada término contribuye al valor total de la expresión, y entender cómo se combinan y operan es fundamental para cualquier tipo de análisis matemático. Así, la identificación y manipulación de términos son habilidades clave para resolver problemas en álgebra y otras ramas de las matemáticas.
Ejemplos de términos: constantes, variables y coeficientes
Los términos pueden clasificarse en diferentes tipos. Por ejemplo, las constantes son números que no cambian y pueden ser positivos o negativos. Algunos ejemplos de constantes son el número 5 o -3. Estas cifras se utilizan en las expresiones para representar valores fijos.
Por otro lado, las variables son símbolos que representan cantidades desconocidas o que pueden cambiar. Comúnmente, se utilizan letras como x o y en expresiones matemáticas. Además, los coeficientes son números que multiplican a las variables. Por ejemplo, en el término 2x, el número 2 es el coeficiente que indica cuántas veces se cuenta la variable x.
Cómo identificar un término en una expresión matemática
Identificar un término en una expresión matemática es una habilidad fundamental en matemáticas. Los términos son los componentes individuales de una expresión, y pueden ser números, variables o combinaciones de ambos. Para identificarlos, es útil observar la estructura de la expresión, separando cada parte según los operadores aritméticos que los conectan, como el signo de suma (+) o resta (-).
Por ejemplo, en la expresión 3x + 5y - 2, los términos son 3x, 5y y -2. Aquí, cada término está separado por los signos de suma y resta. Para identificar términos en expresiones más complejas, como los polinomios, se puede aplicar el mismo principio, reconociendo que cada término se compone de un coeficiente y una variable, o simplemente de un número.
Importancia de los términos en las expresiones matemáticas
Comprender la importancia de los términos en las expresiones matemáticas es esencial para realizar cálculos precisos. Los términos son la base sobre la cual se construyen las operaciones matemáticas, y su correcta identificación y manipulación son cruciales para resolver ecuaciones. Sin un conocimiento adecuado de los términos, es difícil avanzar en áreas más complejas de las matemáticas, como el álgebra o el cálculo.
Cómo los términos afectan el resultado de las operaciones
Los términos en matemáticas tienen un impacto significativo en los resultados de las operaciones. Por ejemplo, en la expresión 3x + 2, si cambiamos el término 2 a 5, la nueva expresión 3x + 5 afectará el resultado de cualquier cálculo que realicemos con ella. Si evaluamos la expresión para x = 2, la primera expresión da 3(2) + 2 = 8, mientras que la segunda resulta en 3(2) + 5 = 11. Esto muestra cómo un pequeño cambio en un término puede alterar el resultado final.
Otro ejemplo se puede observar en la multiplicación. Consideremos la expresión 4xy. Si cambiamos el término 4 a 6, la nueva expresión 6xy producirá un resultado diferente en cualquier operación donde se utilice. Por ejemplo, si x = 3 y y = 2, la primera expresión da 4(3)(2) = 24, mientras que la segunda da 6(3)(2) = 36. Este cambio demuestra cómo los términos influyen en el resultado de las operaciones matemáticas.
La relación entre términos y la simplificación de expresiones
Reconocer y combinar términos es esencial para simplificar expresiones matemáticas. Al juntar términos semejantes, se puede reducir la complejidad de una expresión y facilitar su resolución. Por ejemplo, en la expresión 2x + 3x - 4, los términos 2x y 3x son semejantes y se pueden combinar para obtener 5x - 4. Este proceso de simplificación no solo hace que las expresiones sean más manejables, sino que también permite realizar cálculos más rápidamente.
- Identificar términos semejantes para combinarlos es una técnica clave en la simplificación.
- Utilizar la propiedad distributiva puede ayudar a simplificar expresiones más complejas.
- Reorganizar los términos en una expresión puede facilitar su simplificación.
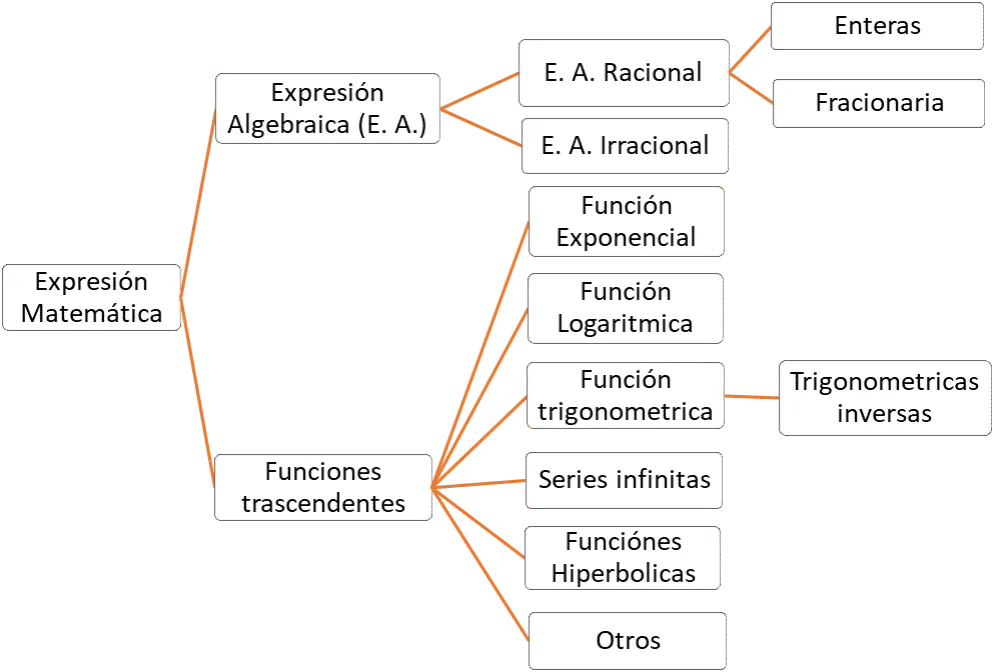
Tipos de términos y sus características en matemáticas
En matemáticas, existen diferentes tipos de términos que se utilizan en las expresiones. Estos términos pueden clasificarse en varias categorías, cada una con sus propias características. Por ejemplo, los términos pueden ser constantes, que son números fijos, o variables, que representan cantidades que pueden cambiar. También hay coeficientes, que son números que multiplican a las variables en un término. Reconocer estas categorías es esencial para comprender cómo se forman y operan las expresiones matemáticas.
Diferencias entre términos homogéneos y heterogéneos
Los términos se pueden clasificar como homogéneos o heterogéneos según sus características. Los términos homogéneos son aquellos que tienen el mismo grado o potencia. Por ejemplo, en la expresión 2x^2 + 3x^2, ambos términos son homogéneos porque tienen el mismo exponente. En cambio, los términos heterogéneos tienen diferentes grados, como en 4x^2 + 5x, donde 4x^2 y 5x son heterogéneos debido a que sus exponentes son diferentes. Esta distinción es fundamental para la simplificación y manipulación de expresiones algebraicas.
La importancia de los términos en álgebra y ecuaciones
Los términos son fundamentales en el ámbito del álgebra, ya que constituyen la base sobre la cual se construyen las ecuaciones. Por ejemplo, en la ecuación 2x + 3 = 11, los términos 2x y 3 son esenciales para encontrar el valor de x. Al resolver esta ecuación, restamos 3 de ambos lados, resultando en 2x = 8, y luego dividimos entre 2 para obtener x = 4. Este proceso ilustra cómo los términos interactúan y afectan el resultado final.
Otro ejemplo se puede observar en la factorización de expresiones algebraicas. Consideremos la expresión x^2 + 5x + 6. Para factorizarla, identificamos los términos y encontramos dos números que multiplicados den 6 y sumados den 5. En este caso, esos números son 2 y 3, lo que nos lleva a la factorización (x + 2)(x + 3). Este tipo de manipulación de términos es crucial en álgebra, ya que permite simplificar y resolver ecuaciones de manera más eficiente.
| Ecuación | Resultado |
| 2x + 3 = 11 | x = 4 |
| x^2 + 5x + 6 | (x + 2)(x + 3) |
Aplicaciones de los términos en la programación matemática
Los términos en matemáticas no solo son fundamentales para resolver ecuaciones, sino que también tienen aplicaciones prácticas en la programación matemática. En el desarrollo de algoritmos y software de análisis de datos, los términos se utilizan para definir funciones y modelos matemáticos. Por ejemplo, al programar un modelo de regresión lineal, cada término de la ecuación representa un componente del modelo, donde los coeficientes indican la influencia de cada variable en el resultado. Esta aplicación permite a los analistas predecir tendencias y comportamientos basados en datos históricos.
Además, el uso de términos en inteligencia artificial y aprendizaje automático es crucial. Los algoritmos de aprendizaje utilizan términos para ajustar modelos a conjuntos de datos, optimizando así la precisión de las predicciones. Por ejemplo, en redes neuronales, cada conexión entre nodos puede ser vista como un término, donde los pesos asignados a cada conexión ajustan la salida del modelo. Esta capacidad de manipular y comprender términos matemáticos es esencial para cualquier profesional que trabaje en el campo de la tecnología y la ciencia de datos, ya que permite la creación de soluciones innovadoras y eficientes.
